※ 본 블로그 포스트는 박지호님의 "Weekly NLP" 내용을 채용하여 개인공부를 기록한 포스트입니다.
원작자의 허가를 맡았으며 불법적인 공유가 아님을 미리 알립니다.
여러분의 이메일 받은 편지함은 얼마나 빨리 쌓이시나요? 저는 이것저것 가입하다 보니깐 하루에도 홍보성 이메일이 수십 개가 오고는 합니다. 저는 앱 아이콘에 숫자가 그려져 있는 것을 견디지 못해서 전부 지우거나 몇 개는 그러다 가끔 읽어보기도 합니다. 중요한 이메일을 놓칠까 봐 조마조마하면서 읽다 보면 시간도 생각보다 많이 낭비되고요.
오늘은 NLP 기술로 여러분의 편지함에서 스팸을 걸러낼 수 있는 감지 모델 (spam detection)을 만들어보려고 합니다. 이미 Gmail 같은 서비스에는 이러한 기술들이 널리 쓰이고 있습니다. 이 글에서는 기본적인 통계 모델 Naive Bayes Classifier를 사용해보려고 합니다.
이것도 이분법(binary classificastion)으로?
6주차에는 문서 분류에 대해서 배워보았습니다. 특히 가장 간단한 0이냐 1이냐의 이분법 (binary classification)을 logistic regression이라는 통계 모델을 가지고 학습시키는 예시를 보았지요. Spam detection도 이분법으로 나눌 수 있을까요?
문제는 우리가 어떠한 데이터를 가지고 있냐입니다. 영화 리뷰를 긍정이냐 부정이냐로 나눌 때에는 부정 (negative; 0)과 긍정 (positive; 1)의 학습/평가 데이터 셋을 가지고 있었지요. 스팸 이메일 역시 이러한 학습 데이터가 필요합니다. 스팸이 아닌 이메일 (negative; 0), 그리고 스팸 이메일 (positive; 1). 이러한 데이터를 가지고 있다면 바로 binary classification 문제로 정의하고 해결책을 찾아볼 수 있습니다.
이렇듯 데이터에 정답(label)이 붙어 있는 것을 Supervised Learning(지도 학습)이라고 합니다.
만약 그러한 데이터가 없다면 어떻게 하냐고요? 그렇다면 두 가지 방법이 있습니다.
첫 번째 가장 쉬운 방법은 지금 이메일함에 들어가서 몇 백개의 이메일을 가져온 다음에 스팸인지 아닌지 직접 분류를 하는 것입니다. 이를 human annotation 또는 data labeling 합니다. 통계 모델을 학습시킬 정도의 규모가 될 때까지 직접 사람이 학습 데이터를 만들어 내는 것입니다.
세상에는 labeling 되지 않은 데이터가 엄청나게 많습니다. 이메일 같은 경우에도 여러분의 편지함에 엄청나게 쌓여 있지만 어떤 것이 스팸인지 아닌지는 labeling 하기 전에는 알 수가 없지요. 이러한 labeling 과정이 보통 머신러닝 모델 개발에 가장 큰 비용과 시간이 들어갑니다. 그렇기 때문에 크라우드소싱을 이용한 crowdworker 서비스를 통해 노동력이 싼 개발 도상국의 인력을 이용하기도 하지요. 이에 대해서는 다른 글에서 다뤄보도록 하겠습니다.
네이버나 구글 같은 서비스들은 유저들이 스팸이라고 신고해주는 데이터를 많이 활용하지 않을까 조심스럽게 예측해봅니다.
두 번째 방법은 anomaly detection이라는 테크닉입니다. anomaly는 변칙이라는 뜻인데, 데이터 전체를 보았을 때 다른 데이터 포인트들과 아주 동떨어진 놈들을 찾아내는 것입니다. 이는 데이터 자체를 보기 때문에 label이 따로 필요하지 않습니다. 다만 데이터의 특성에 따라 성능의 차이가 많이 날 수 있고, 제대로 평가하기가 힘들 수 있습니다. 예를 들어, 저에게 유용한 이메일들이 대부분 비슷한 주제로만 이루어져 있다면, 갑자기 다른 주제인 스팸을 찾아내는 건 쉬울 수 있습니다. 하지만 저의 이메일들이 매우 다양한 주제를 가지고 있다면 이러한 모델로 스팸을 찾아내는 것은 어려울 수도 있습니다.
이 방식은 label이 따로 필요하지 않는 Unsupervised Learning(비지도 학습) 중 하나 입니다.
그렇기 때문에 우리는 데이터가 있다고 가정을 하고 첫 번째 binary classification으로 문제를 접근하기로 합니다.
다시 가방을 꺼내보자
2주차에서 소개한 Bag-of-words (BoW)는 하나의 문서나 문장에 들어 있는 단어들을 순서와 상관 없이 하나의 vector로 표현하는 방식 입니다. 하나의 이메일 역시 이러한 방법을 표현될 수 있습니다.

이번에 소개시켜드릴 모델은 Multinomial Naive Bayes classifier 입니다. 이름은 길지만 사실은 확률과 통계 시간에 배운 베이즈 정리(Bayes Rule) 만 아신다면 매우 쉬운 모델입니다. 베이즈 정리는 Prior probability (사전 확률)와 posterior probability (사후 확률)의 관계를 나타내는 정리인데 기억을 되살리시고 싶으신 분들은 이 블로그를 참조해주시기 바랍니다.
간단한 수학 식을 꺼내서 설명드리겠습니다.
c : classifier가 선택할 수 있는 class (우리의 경우 binary이기 때문에 스팸이냐, 아니냐 두 개의 class입니다)
d : document (이메일)
$$\hat{c} = argmax_{c \in C}P(c|d)$$
위 수식을 말로 풀어 설명하자면 어떤 이메일 (d)이 주어졌을 때, 이 이메일이 스팸인지 아닌지 (c=0? c=1?) 각각 확률을 계산한 후, 더큰 큰 확률을 가진 c를 찾습니다. 수식을 직역해서 말이 조금 어려운데, 결국 "이 이메일 그냥 스팸일 확률이 높아? 아닐 확률이 높아?" 라는 소리입니다.
P(c|d)는 베이즈 정리를 통해 이렇게 바꾸어질 수 있습니다.


그렇다면 남는 것은 이 두 가지 항목인데요:

$P(c)$ : prior probability
조금 더 간단한 P(c) 부분부터 볼까요? P(c)는 이메일(d)과 상관 없이 classifier가 선택할 수 있는 class의 확률, 사전 확률 (prior probability)라고 부릅니다.. 우리에겐 두 가지 옵션이 있습니다 - 스팸이냐 (c=1) 아니냐 (c=0). 어떻게 하면 이 확률을 계산할 수 있을까요?
아주 간단합니다. 그냥 주어진 학습 데이터에서 스팸의 비율이 얼마인지 계산하면 됩니다. 예를 들어 100개의 이메일 중에 2개가 스팸이라는 것을 알면 P(c=1) = 0.02, P(c=0) = 0.98 이 됩니다. 이메일 내용에 대한 아무런 정보가 없다면 이러한 통계를 알고 있는 것이 유용하겠죠?
$P(d|c)$ : Likelihood
Likelihood (가능도)는 어떤 이메일(d)이 스팸 class에서 등장할 가능성을 계산한 숫자입니다. c = 스팸이라고 주어졌을 때, 이 이메일이 작성될 확률을 계산한 것입니다. 조금 헷갈리시죠? 이 이메일이 스팸일 확률을 계산한 것이 아니라, 이미 스팸이라는 가정을 하고 이메일이 쓰여졌다면 얼마나 그럴듯 하냐를 계산한거라 생각하시면 됩니다.
그렇다면 얼마나 그럴듯 하냐는 어떻게 계산할까요. 그건 바로 이메일에 들어가있는 단어 하나하나를 살펴보는겁니다. 혹시 이메일 제목에 "광고", "무료", "보험", "체험", "판매" 같은 단어들이 보이면 바로 스팸으로 여기고 삭제한 경험이 있으신가요? (보험 업종에 종사하시는 분이 있으면 미리 양해 부탁드립니다 ^^)
그것과 같은 원리로 naive bayes classifier는 학습 데이터 중 스팸 이메일들에 들어 있는 단어들에 대한 통계를 확률로 계산합니다. 예를 들어, "보험"이라는 단어가 스팸 이메일 100개 중에 90개에, 보통 이메일의 10개 중에 1번 들어있다고 하면 P(보험 | 스팸) = 90/100 = 0.9로 계산되는 것이지요. 다른 단어들도 각각 이렇게 계산을 합니다.

순진(Navie)하게 단어를 바라본다면?
자, 위의 예시 처럼 각 단어들의 확률을 계산해보았습니다. 하지만 우리가 알고 싶은 것은 이메일(d) 에 대한 확률입니다. 각 이메일은 여러 개의 단어들 (w) 로 이루어져있죠. 단어들의 joint probability (결합 확률)은 어떻게 계산할까요.
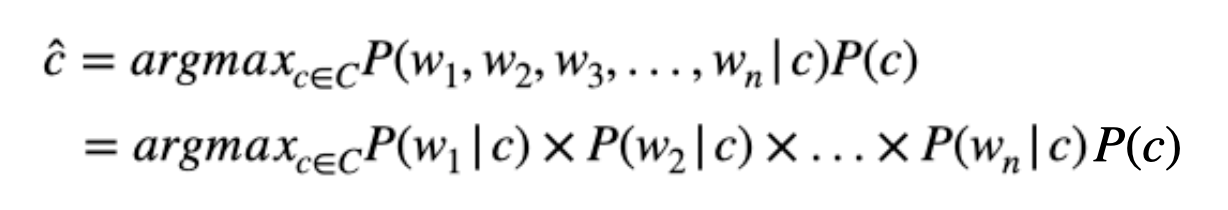
이메일의 joint probability를 제대로 계산하려면 단어의 순서가 중요합니다만, naive bayes classifier는 순서를 무시하고 각 단어들이 independent (독립) 하다는 가정을 넣습니다. 하나의 단어가 발생할 확률이 다른 단어의 영향을 받지 않는다는 것이죠. 사실 이 가정은 이메일 텍스트의 많은 것을 생략합니다. 그렇기 때문에 "naive - 순진하다"라는 이름이 붙은거죠.
하지만 이러한 가정에도 불구하고 간단한 문제에는 꽤나 효과적인 성능을 보입니다. 지난 글에서도 Bag-of-words (BoW) vector가 단순하지만 의외로 좋은 성능을 보인다고 말씀드렸는데, naive bayes classifer가 그 대표적인 예시라고 생각하시면 됩니다.
만약 예측하려는 이메일에 있는 단어에 학습 데이터에 등장하지 않는 것이 나오면 무시합니다. 왜냐면 빈도수가 0이기 때문에 확률도 0이 되기 때문이죠. 그렇다면 joint probability가 항상 0이 되어 문제가 되겠죠?
간단한 예시, "보험 판매 오늘 당장"이라는 이메일을 가지고 마지막까지 계산을 하면 이렇습니다.


결국 "보험 판매 오늘 당장" 이라는 이메일은 스팸인 것으로 예측이 되었습니다.
8번째 포스팅을 시작해보도록 하겠습니다!
일전에 예고한대로 오늘 리뷰하는 내용을 토대로 실력향상을 위한 개인 토이프로젝트를 시도해보려고 합니다.
내용에 대해서는 짧게 다루고 토이프로젝트에 대한 내용을 중점적으로 포스팅하겠습니다.
여러분도 다 아시다시피 텍스트 분류(Text Classification)에는 여러가지 방법이 있습니다.
머신러닝은 "지도 학습", "비지도 학습", "강화 학습" 3가지로 분류되며, 오늘 다룬 나이브 베이즈 정리는 "지도학습"에 해당합니다. 일단은 짧게 베이즈 정리(Bayes' theorem)에 대해 짚고 넘어갑시다.
베이즈 정리(Bayes' theorem)
베이즈 정리는 조건부 확률과 관련된 이론으로 토머스 베이즈에 의해 정립된 이론입니다. 수식은 아래와 같습니다.
$$ P(B|A) = \frac{P(A|B)P(B)}{P(A)}$$
여기서 각 수식의 요소는 다음과 같습니다.
- $P(A)$ : A가 일어날 확률
- $P(B)$ : B가 일어날 확률 (사전 확률)
- $P(A|B)$ : B가 일어난 후에 A가 일어날 확률 (조건부 확률, 사후 확률)
- $P(B|A)$ : A가 일어난 후에 B가 일어날 확률 (조건부 확률, 사전 확률)
▷ 조건부 확률
조건부 확률이란?
<어떤 A라는 사건이 일어났다는 조건>에서 <다른 사건 B가 일어날 확률>을 나타낸다.
이것을 수식기호로 $P(B|A)$로 나타내고, 이해하기 위한 표현을 빌리면 비가 내리는 날에 교통사고가 발생할 확률은 $P(<교통사고>|<비>)$로 나타낼 수 있는 것이다.
▷ 결합 확률과 곱셈 법칙
결합 확률이란?
동시에 일어날 확률을 말한다. 주사위를 던져서 첫 번째가 5, 두 번째가 짝수가 나올 확률을 구해보면 두 경우의 확률의 곱인 $\frac{1}{6} \times \frac{1}{2} = \frac{1}{12}$가 결합 확률이 되는 것이다.
조금만 더 예시를 생각해보면 여러분은 "B와 A의 결합 확률"과 "A와 B의 결합 확률"이 같은것을 알 수 있을 것이다.
이를 변형하면 베이즈 정리가 나음과 같이 나오게 된다.
$$P(B|A) \times P(A) = P(A|B) \times P(B)$$
이제 이 정리를 텍스트 분류에 어떻게 적용하느냐?
이제 우린 베이지안 필터에 대해 알아보자.
나이브 베이즈 분류
베이지안 필터는 나이브 베이즈 분류라는 알고리즘을 사용한다.
어떤 문장을 카테고리 분류할 때 나이브 베이즈 분류는 텍스트 내부에서의 단어 출현 비율을 조사한다.
이를 기반으로 해당 텍스트를 어떤 카테고리로 분류하는 것이 적합한지 알아보자.
실제로 판정을 할 때 $P(B|A)$는 1개의 확률이 아니라 여러 개의 카테고리 중에 어떤 카테고리에 속할 확률이 가장 큰지를 나타내는 정보이다. 즉, 기존 베이즈 정리의 분모에 있는 $P(A)$는 입력 텍스트가 주어질 확률이다. 단, 어떤 카테고리를 판정하든 같은 입력 텍스트가 주어지므로 같은 값으로 생각하면 되기 때문에 고려하지 않아도 된다.
즉, 나이브 베이즈 공식은 아래와 같이 단순화시킬 수 있다.
$$P(B|A) = P(B) \times P(A|B)$$
$P(B|A)$를 생각해보자. 입력 텍스트 A는 단어들의 집합이므로 텍스트를 단어들로 분리한다.
단어가 문서의 어떤 위치에 있다는 정보등을 고려하지 않아도 되는데 이와같이 표현하는 방법이 BoW인 것을 이미 배웠다.
A를 각 단어($a_N$)의 집합이라고 할 때, $P(A|B)$는 다음과 같이 나타낼 수 있다.
$$P(A|B) = P(a_1|B)P(a_2|B)P(a_3|B) \cdots P(a_N|B)$$
$P(a_N|B)$은 단어가 카테고리에 속할 확률이다. 어떤 카테고리에 해당 단어가 출현할 확률을 구하면 되는데 이는 다음과 같이 구할 수 있다.
<단순한 출현율> = <단어의 출현 횟수> / <카테고리 전체 단어 수>
입력 텍스트를 학습시킬 때 출현한 단어가 카테고리에 분류된 횟수를 기억하면 좋다. 실제로 분류를 할 때에는 $P(B) \times P(A|B)$를 각 카테고리별로 계산하면 된다.
가볍게 알아봤으니 이제 프로젝트에 대한 이야기를 해보자.
자세한 것을 프로젝트쪽에서 포스팅하겠지만, 현재 내가 세운 계획을 아래와 같다.
- 단순 Baysian Filter를 이용한 Text Generator 제작
- Vanilla RNN을 이용한 Spam Email Classification 제작
- 이후 모델 개선 ( 파라미터 튜닝, 모델 변화, etc... )
계획된 내용을 가지고 진행 후 회고에 다다르기까지 도전해보겠습니다! :)
자세한 건 프로젝트쪽에서 만나요. 안녕!!
출처 : https://jiho-ml.com/weekly-nlp-8/
Week 8 - 스팸 이메일 분류기 만들기
여러분의 이메일 받은 편지함은 얼마나 빨리 쌓이시나요? 저는 이것저것 가입하다 보니깐 하루에도 홍보성 이메일이 수십 개가 오고는 합니다. 저는 앱 아이콘에 숫자가 그려져 있는 것을 견디
jiho-ml.com
출처 : https://jeongminhee99.tistory.com/73
베이스 정리로 텍스트 분류하기
텍스트 분류 텍스트 분류에는 여러 가지 방법이 사용되는데 자주 사용되는 방법으로는 베이즈 정리를 이용한 "베이지안 필터(Bayesian filter)"가 있다. 학습을 많이 시킬수록 필터의 분류 능력이 오
jeongminhee99.tistory.com
'개발 > NLP Trends' 카테고리의 다른 글
| [후기] 모두를 위한 한국어 오픈액세스 언어모델 못다한 이야기 (feat. 모두연) #2 (1) | 2024.02.10 |
|---|---|
| [후기] 모두를 위한 한국어 오픈액세스 언어모델 못다한 이야기 (feat. 모두연) #1 (1) | 2024.02.09 |
| Weekly NLP #07 Review : 머신러닝과 NLP는 왜 함께 갈까 (0) | 2023.02.23 |
| Weekly NLP #06 Review : 박대리, 얘네 문서들 주제별로 분류해오게 (0) | 2023.02.22 |
| Weekly NLP #05 Review : 얘랑 나랑 얼마나 비슷해? (0) | 2023.02.15 |



